一、树形结构

1、树的定义

树是一种非线性的数据结构，它是由 n(n>=0) 个有限结点组成一个具有层次关系的集合。我们之所以把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

2、基本概念

节点：树中的每个元素称为节点。节点可以有零个、一个或多个子节点。
根节点：树的顶层节点，没有父节点的节点。
边：连接父节点和子节点的线称为边。
度：一个节点的子节点数称为该节点的度。
高度：树中节点的最大层数称为树的高度。
深度：从根节点到某一节点所经过的边的数量称为该节点的深度。

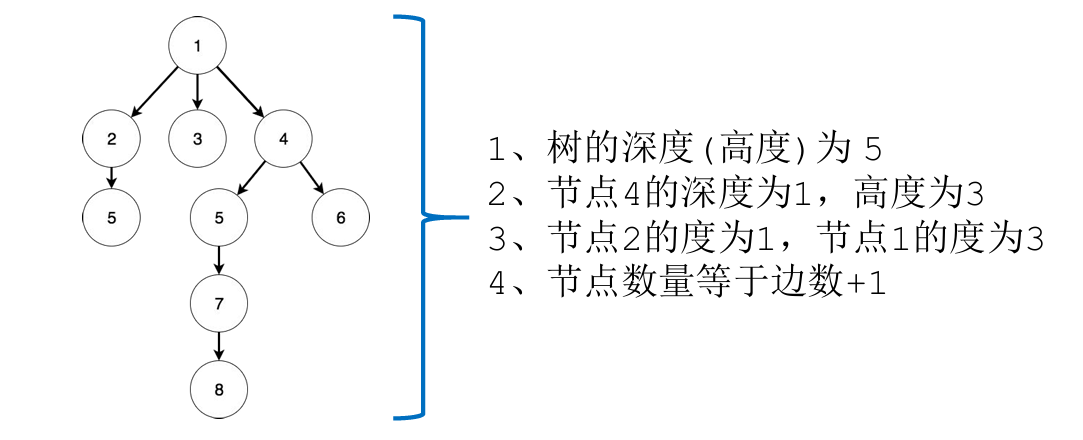
3、重要结论

节点的高度：节点到叶子节点的最长路径（边数）。
节点的深度 = 根节点到这个节点所经历的边的个数。
节点的层数 = 节点的深度+1。
树的高度 = 根节点的高度。

二、二叉树

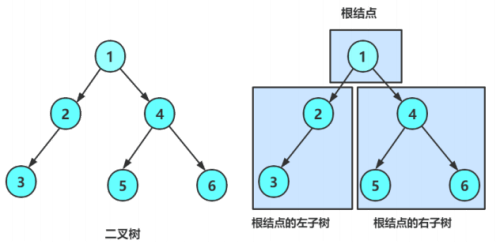
1、结构定义

二叉树的每个节点最多两个子节点，分别是左子节点和右子节点。二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点。

2、二叉树的性质

二叉树的每个节点最多有两个子节点，所以它的度数不超过2。
左子树和右子树是有顺序的，即使节点只有一个子节点，也必须明确它是左子节点还是右子节点。
左子树和右子树也是二叉树，它们本身也遵循上述两个性质。
叶节点是没有子节点的节点，即度数为0的节点。
二叉树中度为0的节点比度为2的节点多一个。

3、代码实现

Ⅰ、结构

定义二叉树节点结构体，包含节点值、左子节点指针和右子节点指针

typedef struct Node {
    int key; //存储值
    struct Node *lchild, *rchild;  //左子节点指针和右子节点指针
} Node;

Ⅱ、新增二叉树的节点

创建新节点并初始化函数，为节点分配内存空间，设定节点值，将左右子节点指针置空

Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node)); //(1)
    p->key = key; //(2)
    p->lchild = p->rchild = NULL; //(3)
    return p;
}

（1）分配内存并创建一个新的 Node 类型的对象。

（2）将传入的参数 key 赋值给新节点的 key 变量。

（3）初始化该节点的左右孩子指针为 NULL。

Ⅲ、销毁二叉树

void clear(Node *root) {
    if (root == NULL) return;//(1)
    clear(root->lchild);//(2)
    clear(root->rchild);//(3)
    free(root);//(4)              
    return;
}

（1）检查节点是否为空，如果为空则返回，终止递归。

（2）递归地清理当前节点的左子树。

（3）递归地清理当前节点的右子树。

（4）释放当前节点的内存。

Ⅳ、插入节点

Node* insert(Node* root, int key) {
    // 检查树是否为空，如果为空，则创建一个新节点作为根节点。
    if (root == NULL) {
        return getNewNode(key);
    }
    
    // 根据键值决定将新节点插入到左子树还是右子树，并递归进行插入。
    if (key < root->key) {
        root->lchild = insert(root->lchild, key);
    } else if (key > root->key) {
        root->rchild = insert(root->rchild, key);
    }
    return root;
}

Ⅴ、广度优先遍历

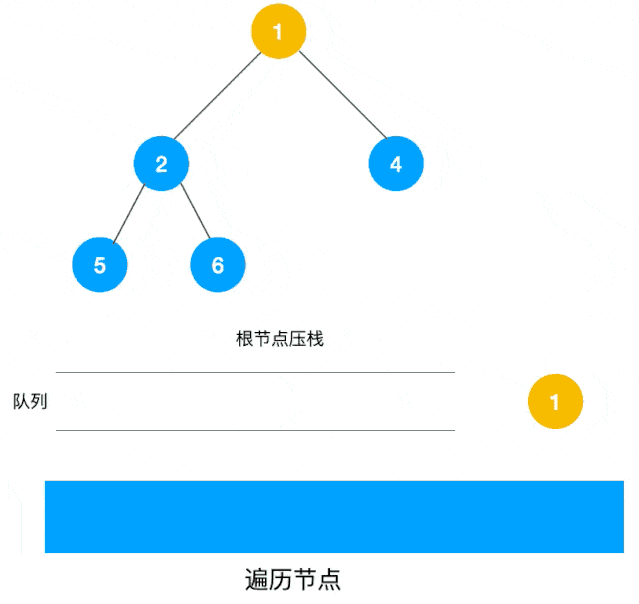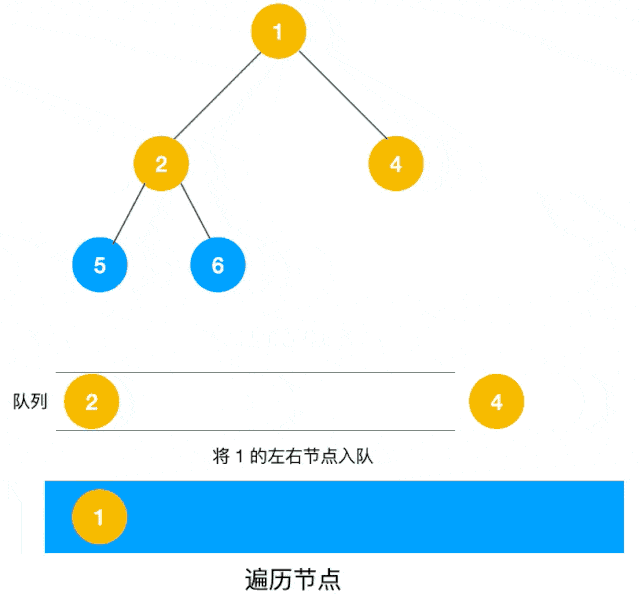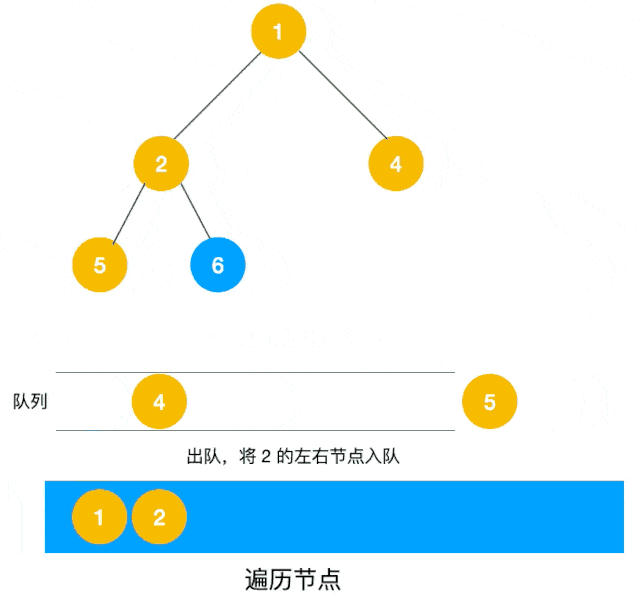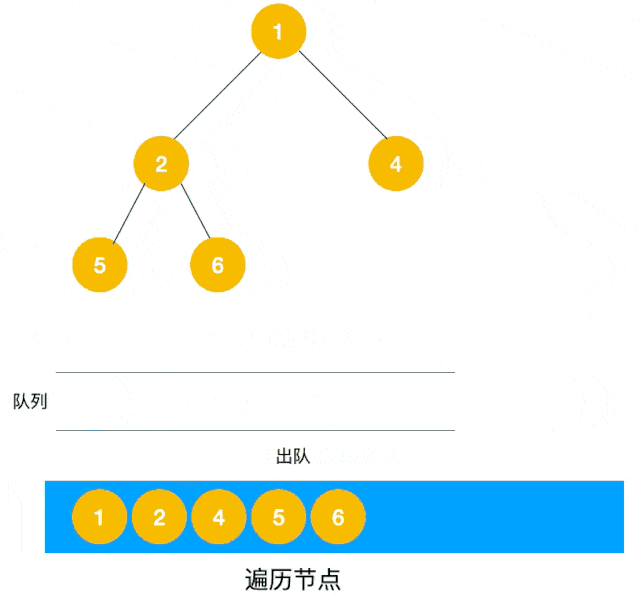
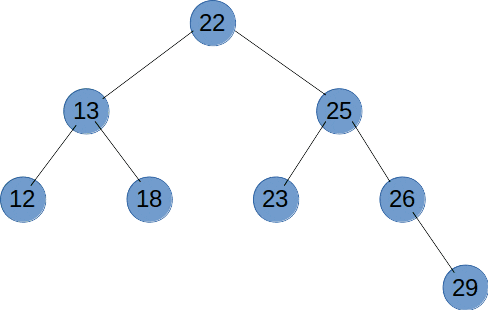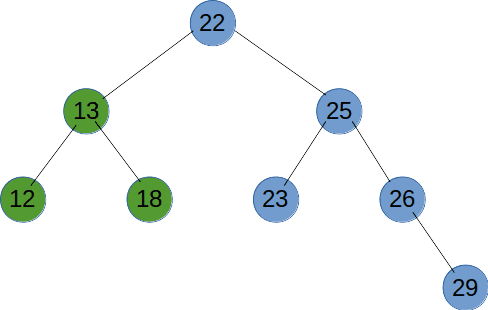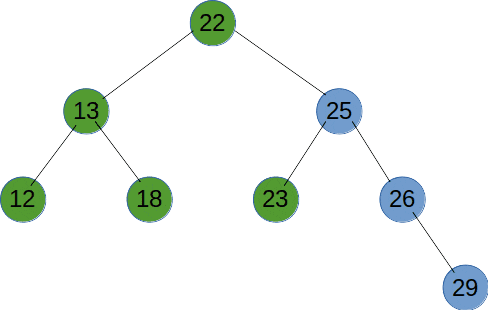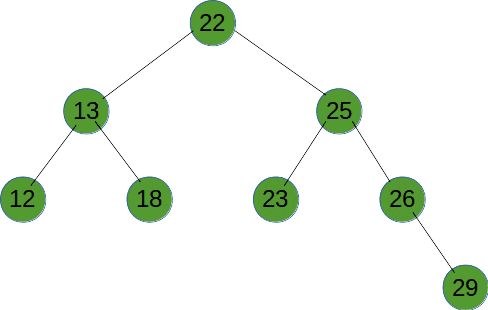
广度优先遍历（BFS）是使用使用队列来实现层次遍历。在 BFS 过程中，队列起到了“先进先出”的作用。当遍历到一个节点时，将其子节点加入队列的尾部。然后，从队列头部取出下一个待处理的节点，继续遍历。这种方式保证了节点按照层次顺序被访问。如下图所示。

// 定义两个整数变量，分别表示队列头部和尾部指针
int head, tail;
// 使用广度优先搜索遍历并打印二叉树节点的函数
void bfs(Node *root) {
    // 初始化队列头和尾指针
    head = tail = 0;
    // 将根节点加入队列
    queue[tail++] = root;
    // 当队列不为空时，继续遍历
    while (head < tail) {
        // 取出队列头部的节点
        Node *node = queue[head];
        // 打印当前节点的值
        printf("\nnode : %d\n", node->key);
        // 如果当前节点有左子节点，将其加入队列中并打印
        if (node->lchild) {
            queue[tail++] = node->lchild;
            printf("\t%d->%d (left)\n", node->key, node->lchild->key);
        }
        // 如果当前节点有右子节点，将其加入队列中并打印
        if (node->rchild) {
            queue[tail++] = node->rchild;
            printf("\t%d->%d (right)\n", node->key, node->rchild->key);
        }
        // 队列头指针后移，表示已处理完当前节点
        head++;
    }
   	    // 函数结束，返回
    return;
}

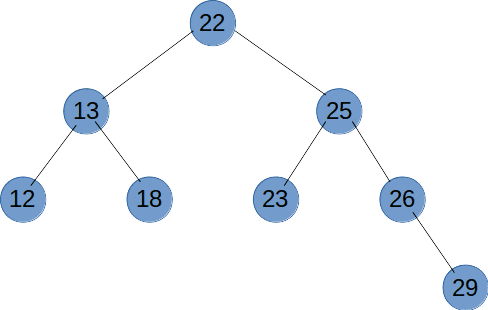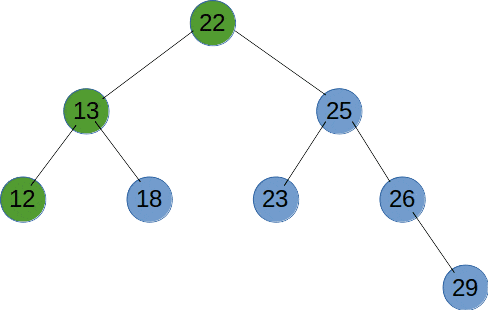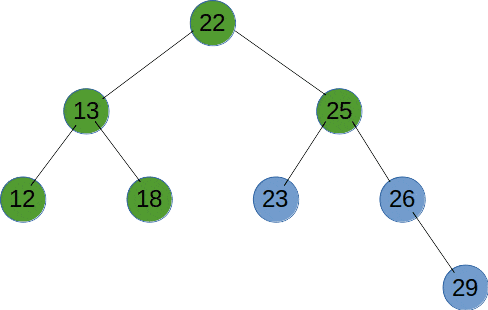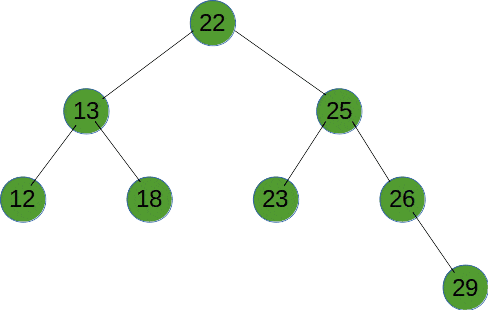
Ⅵ、深度优先遍历

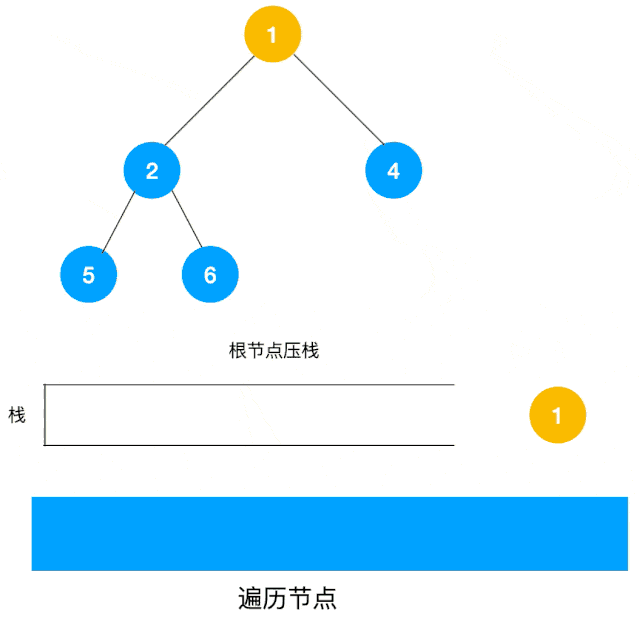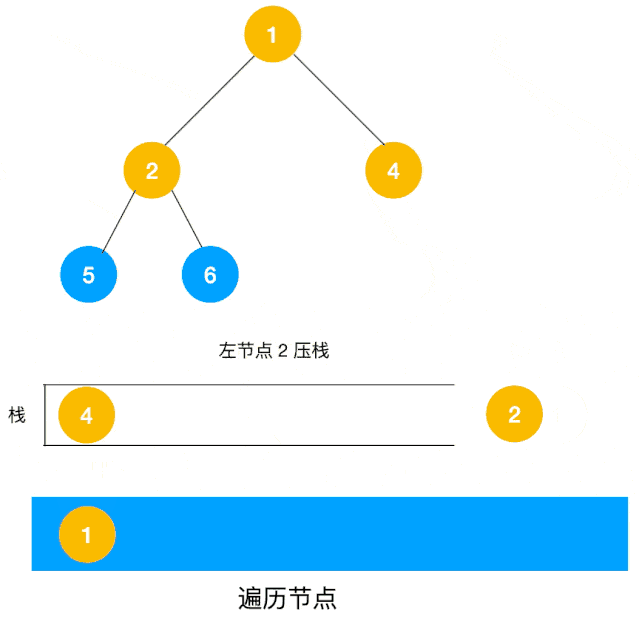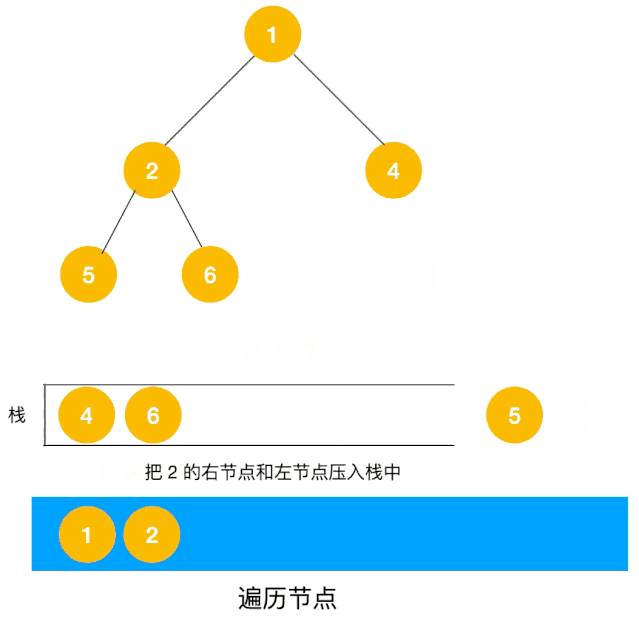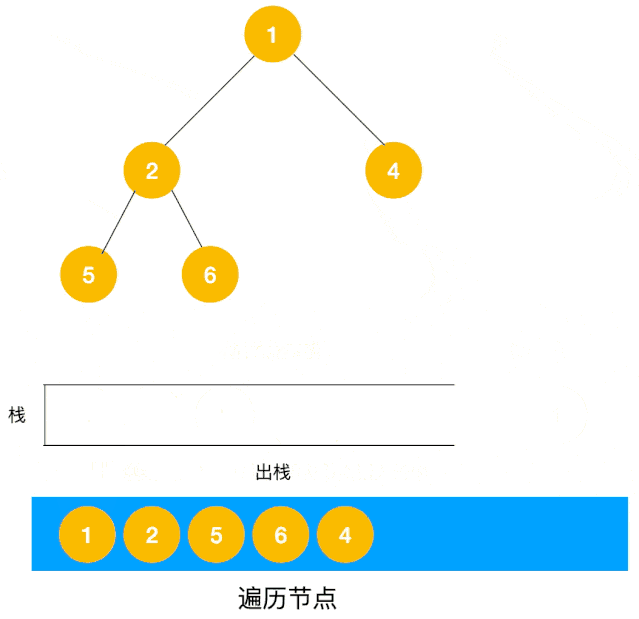
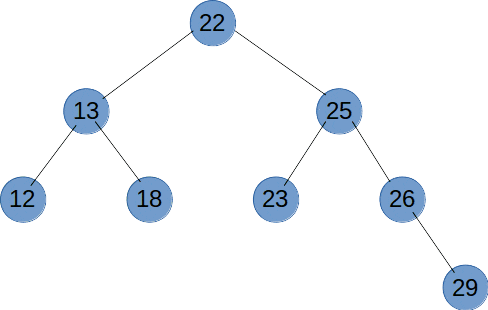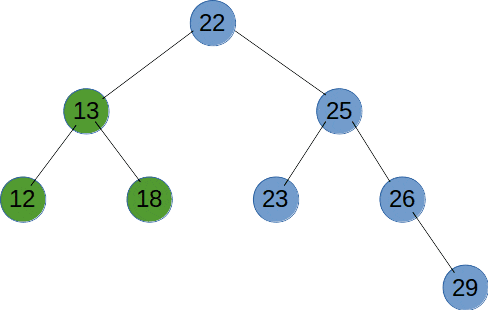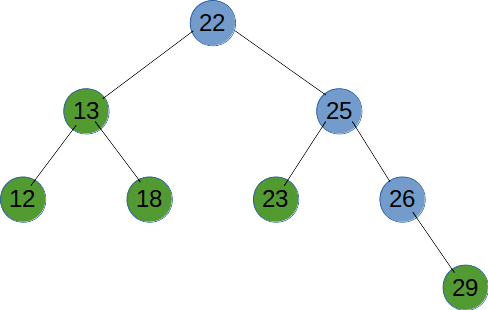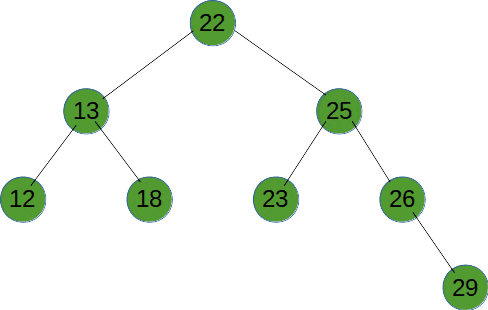
深度优先遍历（DFS）是使用栈来实现遍历，DFS 会从起始节点开始，将其压入栈中。然后，它会弹出栈顶节点并访问其未被访问的相邻节点，将这些节点压入栈中。接下来，它会重复弹出栈顶节点并访问其相邻节点的过程，直到栈为空。

// 定义一个全局变量 tot，用于记录节点访问时间戳
int tot = 0;
// 使用深度优先搜索遍历并计算二叉树节点的访问时间戳区间的函数
void dfs(Node *root) {
    // 如果当前节点为空，直接返回
    if (root == NULL) return;
    // 定义两个局部变量，分别表示节点访问开始和结束的时间戳
    int start, end;
    // 访问当前节点，递增时间戳
    tot += 1;
    // 记录当前节点访问开始的时间戳
    start = tot;
    // 如果有左子节点，递归访问左子节点
    if (root->lchild) dfs(root->lchild);
    // 如果有右子节点，递归访问右子节点
    if (root->rchild) dfs(root->rchild);
    // 访问当前节点的子节点完成，递增时间戳
    tot += 1;
    // 记录当前节点访问结束的时间戳
    end = tot;
    // 打印当前节点的值和访问时间戳区间
    printf("%d : [%d, %d]\n", root->key, start, end);
    // 函数结束，返回
    return;
}

4、二叉树的遍历

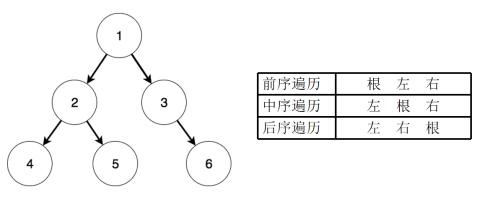
Ⅰ、前序遍历

二叉树的前序遍历是指按照根节点、左子树、右子树的顺序遍历二叉树的所有节点。

// 递归实现前序遍历
// 前序遍历
void preorder(Node *root) {
    if (root != NULL) {
        printf("%d ", root->key); // 访问根节点
        preorder(root->lchild);   // 递归遍历左子树
        preorder(root->rchild);   // 递归遍历右子树
    }
}

Ⅱ、中序遍历

二叉树的中序遍历是指按照左子树、根节点、右子树的顺序遍历二叉树的所有节点。

 // 递归实现中序遍历
void inorder(Node *root) {
    if (root != NULL) {
        inorder(root->lchild);    // 递归遍历左子树
        printf("%d ", root->key); // 访问根节点
        inorder(root->rchild);    // 递归遍历右子树
    }
}

Ⅲ、后序遍历

二叉树的后序遍历是指按照左子树、右子树、根节点的顺序遍历二叉树的所有节点。

 // 递归实现后序遍历
void postorder(Node *root) {
    if (root != NULL) {
        postorder(root->lchild);  // 递归遍历左子树
        postorder(root->rchild);  // 递归遍历右子树
        printf("%d ", root->key); // 访问根节点
    }
}

2022-10-16 该篇文章被子夜打上标签: 数据结构归为分类: 编程手札